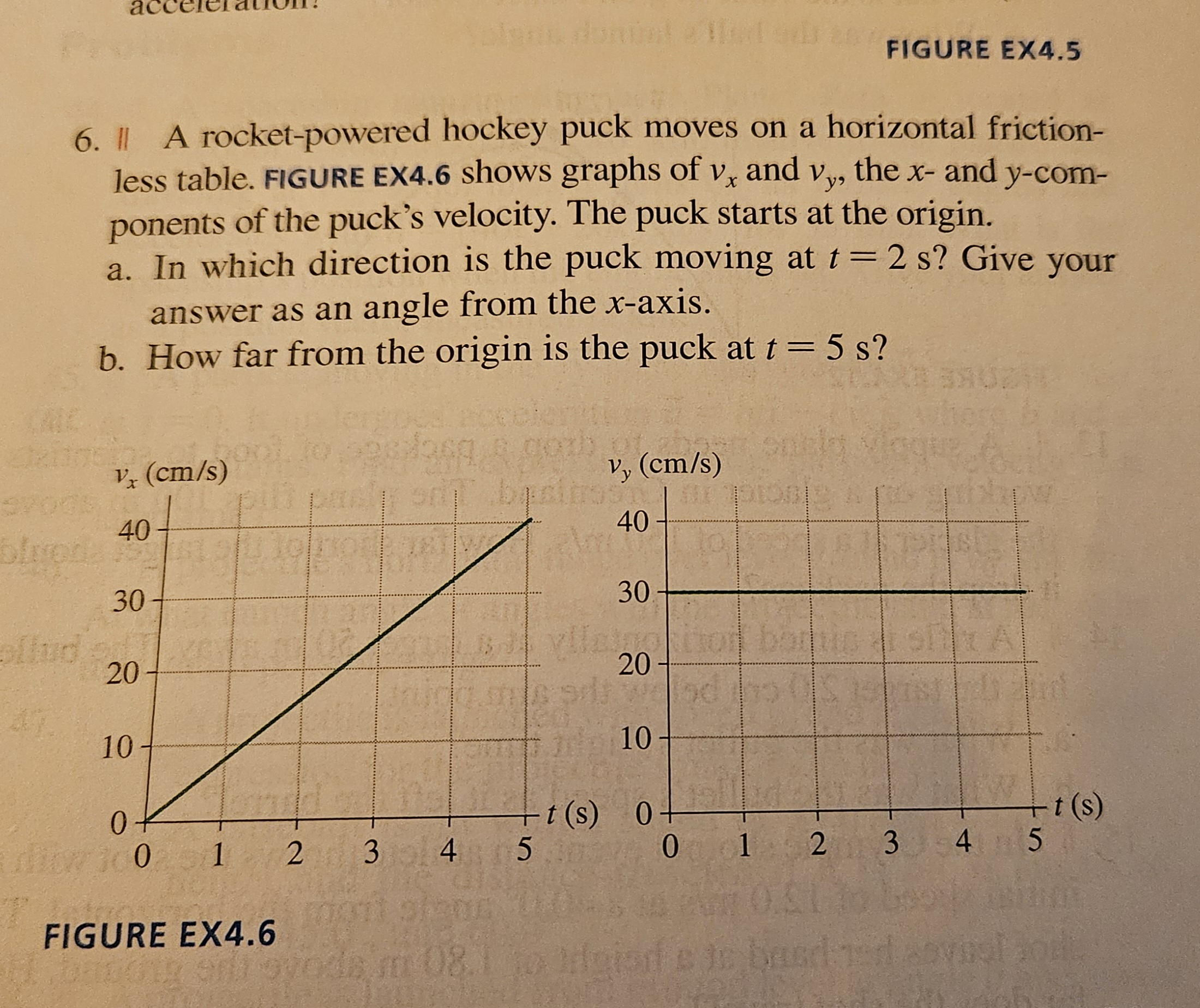Motion in Two Dimensions

Links and useful resources

• START HERE: Physics 2024 class outline
• Physics classroom online interactive tools
• OpenSTAX high school physics
• NotebookLM physics notebook
• Physics projects
• AP Physics 1 Dan Fullerton videos

Lightning Round Questions

• Draw a circuit that uses a pull-up resistor to determine whether a switch is closed or open.

• A circuit has +5v input, then a 1k$\mathrm{\Omega }$ resistor, then a $9k\mathrm{\Omega }$ resistor, then ground. What is the voltage between the resistors?

• What is a control in an experiment? Why is it important?

• Which phase of matter can easily have its volume changed?

• Which phases of matter can easily change shape?

• gr7: [lightning:: 2]

• gr10: [lightning:: 3]

Lightning winner for January: gr10

News..... FROM SPACE

• asteroid with 1:83 chance of hitting earth in 2032
• Asteroid Bennu has 14 of 20 amino acids crucial for life formation

Review

• Motion diagrams: Draw a motion diagram for an arrow shot horizontally from a bow, from the instant it leaves the bow to the instant it touches the ground.
  • Remember to draw the dot spacing increasing as acceleration from gravity increases the vertical component!
  • Remember to draw the velocity vectors between the dots
  • Remember to draw the acceleration vectors at the dots
• Sine and Cosine, rise and run. Review how to find horizontal and vertical components of vectors using angles and trig functions.

Concept summary and connections

• position vector
• instantaneous velocity
• kinematic equations
• average acceleration
• average velocity

Bodies in motion remain in motion, and bodies at rest stay in bed unless their mothers call them to get up.

A neutron walked into a bar and asked, "How much for a gin and tonic?" The bartender smiled wryly and replied, "For you, no charge."

Lesson content with examples

We've used vectors to show the velocity of an object by drawing a motion-diagram. The velocity is just the change in position per unit time though, so what would the position look like if it was drawn as a vector? The answer is that it's just the vector that starts at the origin and goes to the object. If you have two position vectors like that, and you subtract one from the other, you'll get a velocity vector!

So now we can see why the velocity vectors work the way they do in a motion diagram: They're just the result of subtracting an old position vector from the one that follows it.

We also know that we can get acceleration vectors by subtracting the previous velocity from the current velocity.

Kinematic Equations

From our experience diagramming, we learned a few things:

• Velocity is just the change in position over time
• Acceleration is just the change in velocity over time.

Those statements look very similar, don't they? in fact, we can keep going with even more properties of motion (jerk is the next one, and it describes how the acceleration changes...)

Those things can be turned into equations with a bit of thought. We're going to need a way to represent the idea of the change in something in these equations, so here comes some notation: $\mathrm{\Delta }$, the Greek letter Delta, is generally used in physics to mean "the change in." So we'd write $\mathrm{\Delta }x$ to mean "the change in x" over whatever time we're working on.

If we measure position at two times ($t_1$ and $t_2$), we could call them $\overrightarrow{x_1}$ and $\overrightarrow{x_2}$. If we are going to compute the average velocity using those measurements, we'd do it like this: $\frac{\overrightarrow{x_2}-\overrightarrow{x_1}}{t_2-t_1}$. Notice that we subtracted the old value from the new value! That's important, and I guarantee you'll get it backwards a few times because we're so used to doing things in ascending order. If you do it backwards, your velocity will be backwards! Watch out! We physicists are lazy creatures though, and we don't like to write more than necessary. So we're going to write $\frac{\overrightarrow{x_2}-\overrightarrow{x_1}}{t_2-t_1}$ as $\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}$. Whenever you see that, it always means we're computing the change in something.

Now we have a convenient way to write an equation for velocity: $\overrightarrow{v}=\frac{\mathrm{\Delta }\overrightarrow{x}}{\mathrm{\Delta }t}$

We can do something similar for acceleration, which is just the change in velocity: $\overrightarrow{a}=\frac{\mathrm{\Delta }\overrightarrow{v}}{\mathrm{\Delta }t}$

Velocity and position

If you know the velocity and a starting position, you can figure out where the object will be after a time. Remember the rate equation: $d=rt$, which says that distance travelled is equal to the speed (rate) of motion multiplied by the amount time it was moving. That's our first kinematic equation, as long as we remember we're dealing with vectors here and we need to keep track of where we started. We'll use $\overrightarrow{x}$ to represent our position vector, which means $\overrightarrow{x_0}$ is our starting position:

$\overrightarrow{x}=\mathrm{\Delta }t\overrightarrow{v}+\overrightarrow{x_0}$

In other words, multiply our velocity by the amount of time passed, then add it to where we started, and we'll get our new position.

Velocity and acceleration

Acceleration is to velocity what velocity is to position - if you apply acceleration for a while, you get a change in your velocity. So we can use the rate equation again, since what we have is the rate of change of velocity. We'll use $\overrightarrow{v}$ for our current velocity, and $\overrightarrow{v_0}$ for our starting velocity (before the acceleration that we're dealing with happened:

$\overrightarrow{v}=\mathrm{\Delta }t\overrightarrow{a}+\overrightarrow{v_0}$

In other words, multiply the acceleration by the amount of time it was applied, then add that velocity change to the velocity we started with, and you'll get our new velocity.

Position and acceleration

Here's the hard one. If you have just the acceleration, you can use it to see how far you've travelled. The trick here is to realize that we're adding up all of the little changes to velocity that happened over some period of time ($\mathrm{\Delta }t$), but then we still have to multiply it by the time because our position change is a velocity times time! When we get to calculus this will be easier to understand, but for now remember that you multiply acceleration by time to get velocity, and then you mutiply velocity by time to get position, so you can squint your eyes and see how you'd use time squared to go straight from acceleration to position.

Our first crack at this would look like this then: $\overrightarrow{x}=\frac{1}{2}\overrightarrow{a}\mathrm{\Delta }{t}^2+\overrightarrow{x_0}$. Wait, you say, why the half? Remember that we were calculating the average velocity above, and over this time interval, we'd add up the starting and final velocities then divide by two to get the average. That's not the real reason, but it's related so keep that intuitive idea.

Now, that equation is fine as long as we aren't already moving when the whole business gets started. But what if we are already coasting along before the acceleration hits? Can we still figure out where we'll end up? Yes! The thing to remember is that these vector quantities can all be added together, so if we had some velocity before we started, we can just multiply it by the same $\mathrm{\Delta }t$ and add it to the equation:

$\overrightarrow{x}=\frac{1}{2}\overrightarrow{a}\mathrm{\Delta }{t}^2+\overrightarrow{v_0}\mathrm{\Delta }t+\overrightarrow{x_0}$

And there you have it, the path from acceleration to position.

Media resources

• Youtube search for "position vector"
• Youtube search for "instantaneous velocity"
• Youtube search for "kinematic equations"
• Youtube search for "average acceleration"
• Youtube search for "average velocity"

Guided practice

• Do several "find the acceleration vector" problems with motion diagram dots in groups of three (two velocity vectors)

• Draw some position graphs: When is the particle moving "forward"? When is it moving "backward"? When is it at rest?

• Draw some velocity graphs: When is the particle moving forward, backward, and at rest?

• Draw some acceleration graphs: When is it moving forward, backward, and at rest? (can you tell???)

• What is $\mathrm{\Delta }\overrightarrow{x}$ if $\overrightarrow{x_1}=2\hat{ı}+3\hat{ȷ}$ and $\overrightarrow{x_2}=-\hat{ı}-\hat{ȷ}$.

• If those were positions measured a times $t_1=2$ and $t_2=4$, what was the average velocity during that period?

• Say the next measurement was a time $t_3=6$ and the position was $\overrightarrow{x_2}=-2\hat{ı}-2\hat{ȷ}$. What was the average velocity from $t_2$ to $t_3$?

• What was the average acceleration from $t_2$ to $t_3$?

• Spaceship drifting north through the galaxy at 680 m/s. Pilot rotates to 25$\mathrm{°}$ north of east, then accelerates at 75$m/s^2$. Plot the trajectory for the first 20 seconds. (Physics for Scientists and Engineers, p. 85 example 4.3)

• For that example, what is the x-component of the acceleration? What is the y-component?

• Is the spaceship's speed in the "north" direction increasing or decreasing because of the acceleration?

• #hw (physics) Do the "Apprentice level" exercise at this link. It has different ways to describe motion (graph, motion diagram, words, etc) and your job is to look at them all and click on the one that isn't describing the same motion as the others. 2025-02-03

Homework

• #hw (physics) Do the problems on our school page under the Homework heading 2025-01-31

1. For this qustion, read all parts before you start. Draw a pictorial-representation, with all variables present on the diagram, and write the equations you will use to answer the questions
   1. A rocket sled ignites and moves to the right with an acceleration of 30 $\frac{m}{s^2}$ for 5 seconds (where the engine stops). How fast is it moving when the engine stops?
   2. How far did the sled go before the engine turned off?
   3. If the sled now starts coasting with friction so that it decelerates at 5 $\frac{m}{s^2}$ until it stops, how long will it take to stop? How much farther did it go before it stopped?
   4. How far did the sled travel from start to finish?
2. 
3.